12/16/13

Homework: pages 421-422 #13-20 all; 25, 29

Important deadlines:
Dec 18 - All homework/late work due
Dec 19 - TEST!
Dec 19 - Turn textbooks back in (late fee is $5 per textbook per day, so don't forget!)

Rectangles and squares are special types of parallelograms, but not all parallelograms are rectangles or squares.
If two sides are parallel, and the other two sides are parallel, it has to be a parallelogram.
If two sides are parallel and congruent, it has to be a parallelogram.
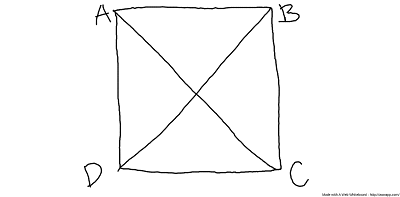
When you connect opposite interior angles in a parallelogram, the line halves must be congruent.

Prove that this is a parallelogram:

Statement                                                             Reason

∠A ≅ ∠C                                                             Given
∠D ≅ ∠B                                                             Given
∠A + ∠B + ∠C + ∠D = 360°                             Definition of a quadrilateral
∠A + ∠B + ∠A + ∠B = 360°                             Substitution
2∠A + 2∠B = 360°                                             Angle addition
∠A + ∠B = 180°                                                  Division property of equality            
Line AD ∥ Line BC                                              Euclid's postulate #5
                                                                                                                      ∎


Solve for x and y.



x = 41, y = 16


Plot these points and determine whether they make a parallelogram or not.
B (0, 0); C (4, 1); D (6, 5); E (2, 4)




FOUR MORE DAYS!

12-11-13

Homework for today: Given sin⊖= .31, cos⊖= .95, tan⊖=1.91
                                  Find cos⊖/sin⊖, find tan⊖, find ⊖, find cos⊖/sin and ⊖

Notes:

Finals week is approaching, young padawans. Remember the wise words of Master Yoda, and do not fear!

12/9/13

No homework today! *hysterical sobbing from students who love math*

A sine deals with a right angle triangle and is opposite over hypotenuse. 

Let's explore with triangles that have no right angles!

sinA = h/c, so c x sinA = h

sinC = h/a, so a x sinC = h

Law of sines (know this for next quiz!):

sinA/a = sinB/b = sinC/c

examples:

sin68°/b = sin37° x b/3

Find distance around the outside:

6/sin32° = x/sin88°

x = 11.3, so distance is 12 + 22.6

math 1050 december 9th 2013

hey lettuce review.

12/4/13

Homework: Ch. 6.4 #6, 7, 8, 9, 27, 58, 59

Reminder: Fill out the class evaluation form for this class! 

See this as an opportunity to inform the administration about Mr. Schiffman's general awesomeness and Jedi Mastery of mathematics.

Practice problem 1: Find the midpoints A, B, and C. (see drawing 1)

A = (-1, 9/2)
    To find the x coordinate, add -3 and 1 together and divide by two. To find the y coordinate, add 8 and 1 together and divide by two. You're just finding the average between the two points!

B = (4, 3)

C = (2, -1/2)

Proof practice: Prove that ∆ABC is congruent to ∆XYZ (see drawing 2)
Hint: Remember to use AA.

Practice problem 2: Solve for x (see drawing 3)
     Answer:
                 25/x + 20 = 12/-3x
                 25(-3x) = 12 (x + 20)
                -75x = 12x + 240
                -87x = 240
                 Divide both sides by -87

for master yoda and his excellent modeling.

MATH 1050 December 4th 2013

REMEMBER STAY ON TOP OF HOMEWORK AND QUIZZES

YOUR TEST WILL BE OVER CONIC SECTIONS AND SUMMATIONS. SOMETIME NEXT WEEK.

THE 18TH AND 19TH ARE THE DAYS OF THE FINAL EXAM.

MONDAY DEC. 16TH- LAST DAY FOR WEB ASSIGN HOMEWORK.

WEDNESDAY DEC. 11TH- LAST DAY FOR QUIZZES.
_________________________________-____________________________________________

quote from miles hubbard,"so one circle becomes two."

12/3/2014 - Secondary 2 Homwork

6.4: 15, 19, 23-26 (all), 33, 53

12/2/13

Homework: Page 302 #11-21 odds, 29

Remember these dates, dear UCASians. Your grades depend on it.

Friday, Dec. 6 - Quiz
Friday, Dec. 13 - Quiz
Thursday, Dec. 19 - Test
Wednesday, Dec. 18 at 4:00 - The final deadline for turning in assignments.

Proofing practice!

Prove that ∆ABC ≅ ∆QDE

Statements                                  Reasons
Line AC ∥ line DQ                       Given
Line ED ∥ line BC                       ∠GEF ≅ ∠CFE, if alternate interior angles are congruent, then the                                                              lines are parallel because the corresponding angles are congruent.
∠FCE ≅ ∠GEA ≅ ∠GDB         Corresponding angles/Alternate interior angles
∠FEG ≅ ∠GBF                          Euclid's postulate #4
Line ED ≅ line CB                       Reflexive argument based upon line AC ∥ line DQ and
                                                    line ED ∥ line BC are parallel
∆ABC ≅ ∆QDE                           ASA

math 1050 december 2nd

9.1

STAY ON TOP OF THIS HOMEWORK. PLS.

summations and sequences

11/20/13

Homework: Ch. 6.1 #7-27 odds, 41

Can you factor this? 6x² + 11x + 3

Sure, you can do it algebraically, but you can also channel your inner ancient Greek and solve it using geometry. See drawing at bottom.
The answer is (3x + 1)(2x+3).

Ratios are comparisons between two like units. For instance, in this class, the ratio of males to females is 11:14 (that's in colon notation. There are no units because they cancel out.)
Rates are fractions that compare two unlike units. Ex: 30 miles/hour, 3 dollars/pound, etc.
If they can be reduced, reduce them. Don't leave any radicals in the denominator. Write them as fractions!

Proportions are equations where a rate equals a rate, or a ratio equals a ratio. You can cross-multiply to get your answer with proportions. Ex: 30 miles/hour = x miles/5 hours. (x = 150)

Practice problems:
If 8,218 schools have 270,272 girls, what is the rate of girls per school? Round answers to the nearest tenth.
Answer: 270,272 girls/ 8218 schools = 32.9 girls/school.

3,122 people smoke cigarettes. 1,615 of those people quit smoking. What is the ratio of those that smoke to those that don't?
Answer: 3,122 - 1,615 = 1,507 smokers left. The ratio of those that smoke to those that don't is 1,507/1,615 or 0.9 or (best answer) 9:10.

A triangle's side proportions are 4:6:9, and its perimeter is 190 inches. What are the lengths of its sides?
Answer: 4 + 6 + 9 obviously doesn't equal 190 inches, so look at it like 4x + 6x + 9x = 190. x=10, so the side lengths are 40, 60, and 90.

A triangle's side proportions are 3:2:8 and its perimeter is 72. What are its side lengths?
Answer: 3x + 2x + 8x = 72. 13x = 72, and x = 5.54. So 3(5.54), 2(5.54), and 8(5.54) are the side lengths.

The replica of a statue is 10 inches tall. The real statue is 10 feet tall. What is the ratio of the replica's height to the statue's?
Answer: Convert 10 feet to inches. So 10 in/10 feet = 10 in/120 in. Simplifies to 1/12.

November Something 2013 Math 1050

Padawons. Much to learn there is.


Hk format is just slope intercept format- just danced around.

That's all I have for you today.

11/18/13

Homework: Ch. 4.1 page 181 #21-29 all.

Lots of big things approach, young padawans. On December 19, you have a test! From this point on, each quiz you have could drop the score of a previous, lower quiz score. (Your five highest scores will go on your grade.)

Notes for today:

Triangle classification by angles (see drawing one):
 - If an angle in a triangle is greater than 90 degrees, it's an obtuse triangle.
 - If an angle in a triangle is exactly 90 degrees, it's a right angle triangle, or normal triangle.
 - If all three angles of a triangle are less than 90 degrees, it's an acute triangle.
 Note: α = Alpha, β = Beta, γ = Gamma, δ = Delta

Triangle classification by sides (see drawing two):
 - Equilateral triangles have equal sides and all angles measure 60 degrees.
 - Isosceles triangles have two equal sides and two equal angles.
 - Scalene triangles have no equal sides and no equal angles.
Note: All equilateral triangles are also isosceles triangles, but not all isosceles triangles are equilateral triangles. Like rectangles and squares!

With congruent triangles, all sides and all angles must have the same measure.
With similar triangles, all angles must have the same measure, and the proportions of the sides must be the same.

A dilation makes a shape bigger.
A contraction makes it smaller.

ALL parabolas are similar! Just so you know.

AA (Angle Angle) is not something you can use to prove congruency.

In-class proof (see drawing #3)

math 1050 november 18th 2013

We went over the test today. O_O GOOD JOB YOUNG PADAWONS! Chapter 8 your next test is on monday, the twenty fifth. BUT DON'T CRY BECAUSE YOU GUYS ARE LAZY AND GET THOSE PINK SHEETS THAT GIVE YOU ALL OF THE FREAKING EQUATIONS. =.= and because I, jedi master kristen, am so frustrated- NO NOTES FOR YOU. I HOPE YOU PAID ATTENTION IN CLASS. have a nice day. WITHOUT MY HELPFUL NOTES.

11/13/13

Your homework for today is to finish proof #3.

Link to proof examples

11/11/13 MATH 1050

TEST ON FRIDAY

kristen's notes for the day
p.s. the lattice method is only used for 3x3 matrices

11/6/13

Look! A worksheet just for you! :)

Good luck on your test, everyone.

abstract art

by, jedi master kristen

to, master yoda

reminds me of my lost childhood; when  I didn't know the quadratic formula.

miles says do you homework.

shout out to miles hubbard, the respectable biologist. 

11/4/13

Homework for 10.6: #9-19 all.

Starting with your next quiz, Mr. Schiffman will drop your lowest quiz score, so do well on it in order to raise your grade!

YOUR TEST IS ON FRIDAY. Be prepared. It will cover chapters 10.1 to 10.7.

Example problems:

11/4/13 MATH 1050

Next test: November 15th

Important Definitions to take into consideration:

• Matrices: are a man made contrivance. -Master Yoda
• Matrices are always identified as capital letters. ex: A= [     ]
• AxB DOES NOT ALWAYS EQUAL BxA 
• BUT... A+B =  B+A 

1. Gauss Elimination: the process to put  a matrix in row echelon form.
2. Gauss-Jordan Elimination: the process of puttin matrix in REDUCED row echelon form.
3. Row Echelon Form (see picture)
4. Reduced Row Echelon Form (see picture)

EXAMPLE OF HOW TO SOLVE A MATRIX (DONE IN CLASS):